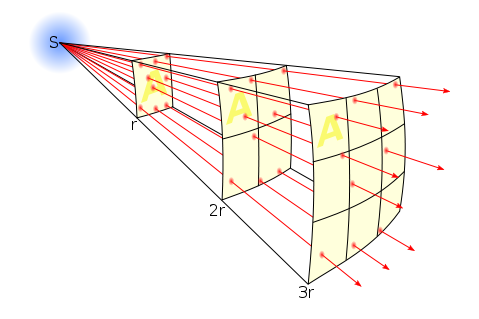
Inverse Square Law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or intensity is inversely proportional to the square of the distance from the source of that physical quantity. In equation form:
\mbox{Intensity} \ \propto \ \frac{1}{\mbox{distance}^2} \,
The divergence of a vector field which is the resultant of radial inverse-square law fields with respect to one or more sources is everywhere proportional to the strength of the local sources, and hence zero outside sources. Newton’s law of universal gravitation follows an inverse-square law, as do the effects of electric, magnetic, light, sound, and radiation phenomena.
Acoustics
In acoustics one usually measures the sound pressure at a given distance r from the source using the 1/r law.[9] Since intensity is proportional to the square of pressure amplitude, this is just a variation on the inverse-square law.
Example
In acoustics, the sound pressure of a spherical wavefront radiating from a point source decreases by 50% as the distance r is doubled; measured in dB, the decrease is still 6.02 dB, since dB represents an intensity ratio. The behaviour is not inverse-square, but is inverse-proportional (inverse distance law):
p \ \propto \ \frac{1}{r} \,
The same is true for the component of particle velocity v \, that is in-phase with the instantaneous sound pressure p \,:
v \ \propto \frac{1}{r} \ \,
In the near field is a quadrature component of the particle velocity that is 90° out of phase with the sound pressure and does not contribute to the time-averaged energy or the intensity of the sound. The sound intensity is the product of the RMS sound pressure and the in-phase component of the RMS particle velocity, both of which are inverse-proportional. Accordingly, the intensity follows an inverse-square behaviour:
I \ = \ p v \ \propto \ \frac{1}{r^2}. \,